Digitaalisen oskilloskoopin alias ilmiöt. Osa 2.

Teoriaa ja käytäntöä alias ilmiöstä joka on usein esillä puhuttaessa digitaalisista oskilloskoopeista. 

Tässä osassa 2. otetaan esiin erityisesti aliakset liittyen FFT käyttöön.

Asiaa käsitellään seuraavassa lähinnä SDS1204X-E oskilloskooppi esimerkkinä.
Luonnollisesti samat asiat sovellettuna sopivat muuhunkin kun huiomoi toisenlaiset spesifikaatiot.

Nykyaikaisissa oskilloskoopeissa myös FFT ominaisuudet ovat kehittyneet huomattavasti aiemmista myös edullisemman pään oskilloskoopeissa. Nyt kun FFT alkaa olla oikeasti käyttökelpoinen hiukan vaativampiinkin tarkoituksiin on syytä hiukan tarkastella alias ilmiötä sen kannalta. Esimerkiksi Siglent SDS1000X-E sarjan FFT käyttää maksimissaan 1M näytettä. Aikaisemmin edullisissa oskilloskoopeissa FFT saattoi pohjautua esimerkiksi 2k - 16k määrään näytepisteitä jolloin taajuusresoluutio jää varsin alhaiseksi.

Aliasointiin ja samplenopeuteen liittyvät perus ilmiöt on erittäin tärkeää ymmärtää käytettäessä FFT toimintoa.

Suosittelen vilkaisemaan ensin tai tämän rinnalla:
Digitaalisen oskilloskoopin alias ilmiöt. Osa 1.

Joissain kohdin pistän hiukan mutkia suoraksi, kuitenkin niin että valtavia vääristymiä ei synny, muuten pitäisi kirjoittaa kirja.

Yksinkertainen kertaus: Oletetaan että AD muunnin ottaa tasavälein näytteitä jatkuvasti jollakin näytetaajuudella. Kaikki signaalin taajuuskomponentit jotka pääsevät AD muuntimeen ja ovat taajuudeltaan suurempia kuin puolet näytetaajuudesta muodostavat aliaksen. (Kuva 1.)
Ei ole mitään keinoa estää sitä tai vähentää sitä. Jos joku sellaisesta puhuu hänellä on käytössään joku ns "vaihtoehtoinen totuus" tai sitten puhe ymmärretään väärin. Käytännössä ongelmat alkavat jo jonkun verran alempana kuin näytetaajuus/2.

Seuraava koskee nimenomaaan ja vain ns "real time" oskilloskooppia. Sellainen ottaa käytössä olevalla samplenopeudella yhdellä vaakapyyhkäisylla kaikki näytteet tasavälein. Puhutaaan myös ns "single" shot samplenopeudesta.

Yksinkertainen piirros siitä mistä alias ilmiössä on kyse.


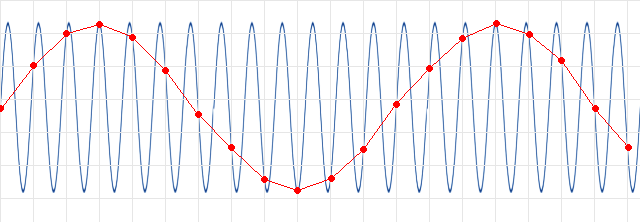
Kuva 1.
Kun signaalin taajuus on suurempi kuin näytetaajuus (punaiset näytepisteet) ei alkuperäistä signaalia voida rekonstruoida näytepisteiden pohjalta. Sen sijaan muodostuu "alias" siniaalto mutta sen taajuus on aivan väärä.

Nyquist-Shannon teoreeman mukaan näytetaajuuden tulee olla vähintään kaksinkertainen signaalin taajuuteen nähden (fNyquist = fsample/2). Jotta silloin voitaisiin rekonstruoida signaali pitää täyttää monta tiukkaa ehtoa. Niitä ei kaikkia täytetä missään tiedossani olevassa oskilloskoopissa. Tulee siis pysyä reilulla etäisyydellä fNyquist alapuolella.

Alias taajuuksien kannalta Nyquist taajuus ( fN ) on aivan olennainen. Se on sellainen ns ehdoton raja. Kaikki se mitä on fN yläpuolella muodostaa alias taajuuden. AD muunnin on myös taajuuden alaspäin muunnin.

Esimerkiksi jos AD muuntimen näytetaajuus olisi 200MHz (200MSa/s) olisi fN tällöin 100MHz. Mikäli AD muuntimen sisääntuloon tuotaisiin nyt 110MHz saataisiin ulos 10MHz. Ainoa keino estää tämä on se että estetään kaikkien yli fN taajuuksien pääsy AD muuntimen sisääntuloon. (kokonaan eri asia on jos puhutaan desimoidusta näytenopeudesta ja aliasoinnista sillä taajuudella ja jos AD muuntimen todellinen näytetaajuus on korkeampi ja sillä taajuudella aliasointia ei tapahtuisi.  Olisi periaatteessa mahdollisuus filtteröidä ennen desimointia, mutta tällaista ei ole käytössä tässä tapauksessa)

Seuraavassa kuvassa on vastaavasti esimerkki 1MHz näytenopeudesta.
Signaalin taajuus 900kHz. Samplenopeus 1MSa/s. Tästä puolet, eli Nyquist raja, on 500kHz.
Tämä on esimerkki klassisesta perus alias ilmiöstä joka on usein esimerkkinä.

Alhaista näytenopeutta ja alhaista taajuutta käytetty esimerkkinä vain jotta on ollut helpompi demonstroida. Sama matematiikka toimii tietenkin taajuuuksien ollessa toiset.

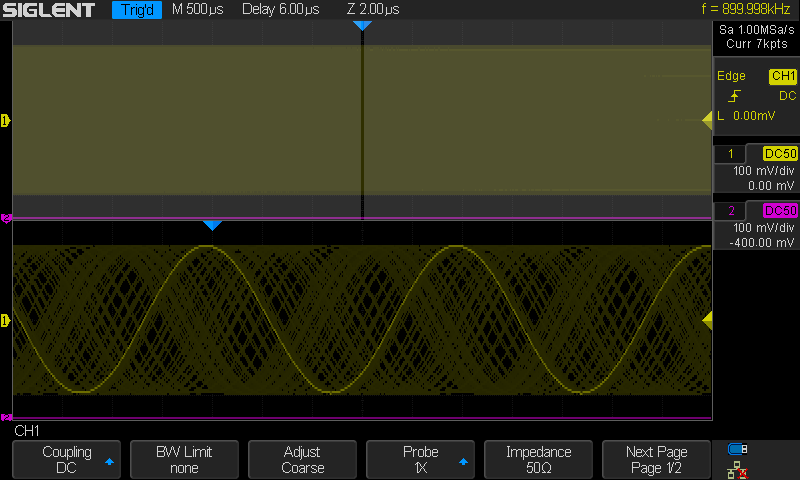
Kuva 2.

Kuvassa 2. näkyy 100kHz siniaalto. Signaali on 900kHz sini. (poikkeuksenä tämän kuvan skooppi on SDS1000X+ sarjalainen)
Sampletaajuus 1MHz. Signaali 900kHz. Nyquist raja on 500kHz. Jos katsoisi tätä tilannetta FFT analysaattorilla. Sekin näyttäisi 100kHz signaalia. (sampletaajuus - sisääntulotaajuus)

SDS1204X-E (samoin kuin SDS1202X-E) ovat 200MHz oskilloskooppeja mutta taajuusalue ylettyy huomattavasti ylemmäs mutta poikkeuksellisen hitaasti vaimentuen mentäessä taajuudessa ylöspäin. Kun oskilloskoopin maksimi näytetaajuus on 1GHz (1GSa/s) on vastaavasti FFT maksimialue 0-500MHz.  Pitäisi vaimentaa aliaksia mutta pitäisi tarjota kuitenkin esim FFT käyttöön taajuusvastetta mahdollisimman ylös ja sitten ei kuitenkaan saisi syntyä aliaksia. Kun ei lisätä kallista rautaa ollaan helposti sen edessä että on tehtävä aika rankkoja kompromisseja. Joka tapauksessa kun mennään alemmille näytetaajuuksille joka tapauksessa törmätään aliasten mahdollisuuteen.
Siksi, käyttäjän on tiedettävä asia ja käyttäjän on osattava hallita asia tai ainakin osata kiertää pahimmat ansat ettei mene ns "helppoon". Pääsääntö FFT käytössä: Pyri estämään että sisään AD muuntimelle saakka ei tule merkittävällä signaalitasolla taajuuskomponentteja jotka ovat suurempia kuin näytetaajuus/2 eli suurempia kuin fN

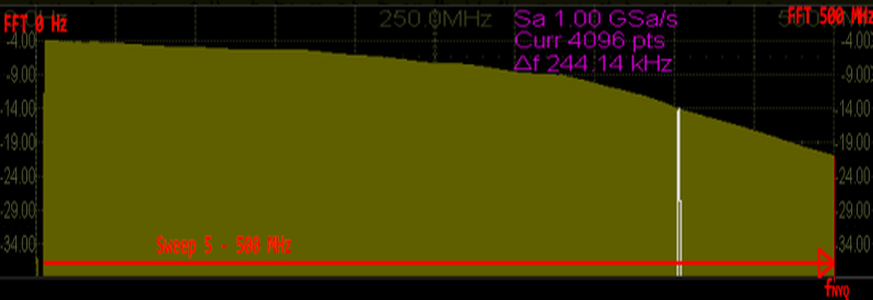
Kuva 3.

Huomaa että tässä mittauksessa 200MHz oskilloskoopin signaalitaso on tippunut noin 17dB taajuudella 500MHz joka on 1GSa/s näytenopeuden fN taajuus.
Mikäli näytenopeus olisikin 500MSa/s (useampia kanavia käytössä tai muu syy) olisi fNtaajuus 250MHz ja vaimennus vain luokkaa 3dB.

Seuraavaksi otan esimerkin jossa FFT käytössä ja pyyhkäistään hyppimällä 10MHz - 1GHz. FFT samplenopeus 1GSa/s. Kuva ei ole kaunis. Kuvassa on pääasia ollut että samaan kuvaan saa  myös alias taajuudet tai jonkunlaisen kuvan niistä kun signaalin taajuus kasvaa yli Nyquist rajan ja siten ettei ne peity tuon 10 - 500MHz osuuden alle piiloon. Kuvassa siis on FFT asetettu ns Max-Hold tilaan jolloin se pitää siihen asti kertyneen maksimin näytöllä.

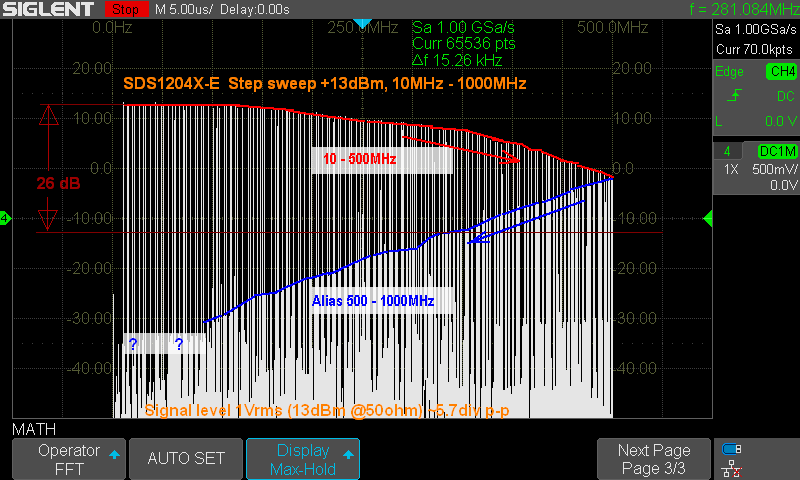
Kuva 4.
Näytetaajuus 1GHz. Kun taajuuspyyhkäissy etenee kohtaan 500MHz (fNyquist) sen jälkeen signaalin taajuus alkaa laskea näytöllä (se on alias taajuus)
Esim kun signaalin taajuus on 510MHz on sen alias 490MHz ja signaaligeneraattorin taajuuden edelleen noustessa esim 800MHz on sen taajuuden alias 200MHz ja niin edelleen.

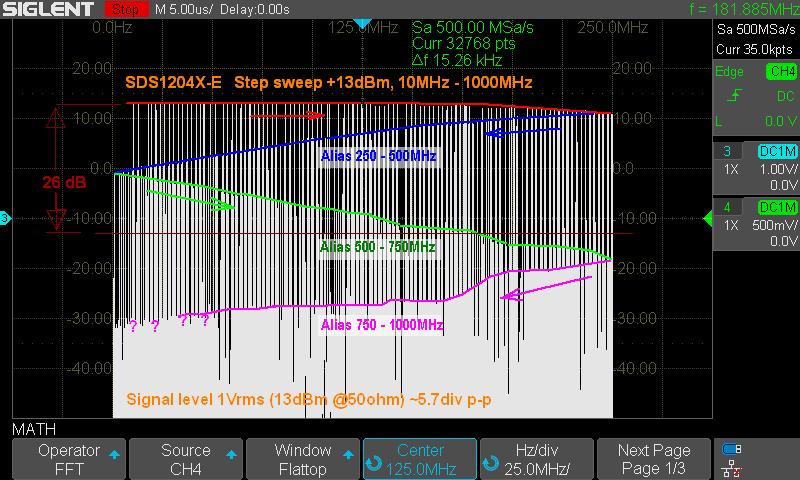
Kuva 5.
Näytetaajuus 500MHz. Kun taajuuspyyhkäissy etenee kohtaan 250MHz (fNyquist) sen jälkeen signaalin taajuus alkaa laskea näytöllä (se on alias taajuus kunnes tulklaan seuraavaan käännekohtaan(0)  ja alias alkaa taas kasvaa,)
Esim kun signaalin taajuus on 260MHz on sen alias 240MHz (sininen) ja signaaligeneraattorin taajuuden edelleen noustessa esim 490MHz on sen taajuuden alias 10MHz (Vihrea) ja niin edelleen. Kun sitten edelleen jatketaan ja taajuus on 550MHz on sen alias taajuus 50MHz (Vihreä) ja kun saavutaan taajuuteen 740MHz on alias 240MHz (Vihreä) ja edelleen kun taajuus on 800MHz on alias 200MHz (punainen) jne. Voi tuntua mutkikkaalta mutta kun asian ymmärtää niin alkaa selvitä miksi FFT kuva on joskus hyvin kummallisen tuntuinen kun oikeat taajuudet, aliakset ja harmonisten taajuudet ja niiden aliakset ovat kaikki yhtenä "kaaoksena" näytöllä. ja tulee sitten niitä ilmöitä kun taajuus nousee niin joku piikki FFT siirtyy alaspäin ja joku ylöspäin taajuudessa.
Mitään tällaista ei ilmene mikäli sisään AD muuntimelle saakka ei pääse mitään taajuuskomponenttia joka ylittää Nyquist taajuuden. Siksi: Pyri kaikin keinoin estämään niiden pääsy AD muuntimelle. Jos niitä pääsee, yritä ymmärtää että jotkin näkyvät taajudet näytöllä ovat totta ja jotkut alias taajuuksia.

Kuten todettu, AD muunninta voi myös käyttää taajuusmuuntimena. ;)

Luonnollisesti kannattaa hyödyntää esimerkiksi 20MHz BW filtteriä joka skoopissa on, silloin kun sen käyttö sopii tutkittavan kannalta. Samoin muun muassa probea voi käyttää "filtterinä". Muistetaan että 1x asennossa tavallisen 1x/10x proben taajuusvaste on usein alle 10MHz.
Lisäksi proben käyttöä LPF filtterina voi "jalostaa" hiukan lisää varsin laajoissa rajoissa hyvinkin yksinkertaisesti.
Täälläkin yksi esimerkki.

--»  Ylös 

--»  Oskilloskoopit

--»  Etusivulle - Home